Tia Phân Giác và Đường Phân Giác: Khái Niệm, Tính Chất và Ứng Dụng Chi Tiết

Trang Chủ / Kiến thức / Tia Phân Giác và Đường Phân Giác: Khái Niệm, Tính Chất và Ứng Dụng Chi Tiết Bài Mới

Trong hình học, tia phân giác và đường phân giác là những khái niệm nền tảng, đặc biệt quan trọng khi nghiên cứu về góc và tam giác. Việc hiểu rõ về chúng giúp giải quyết nhiều bài toán phức tạp và có ứng dụng trong nhiều lĩnh vực khác nhau. Bài viết này sẽ đi sâu vào định nghĩa, cách xác định, các tính chất nổi bật và ứng dụng thực tiễn của tia phân giác và đường phân giác, giúp bạn nắm vững kiến thức này.

Nội Dung Bài Viết

Tia Phân Giác Là Gì?

Trong hình học phẳng, tia phân giác của một góc là một tia xuất phát từ đỉnh của góc và nằm giữa hai cạnh của góc, chia góc đó thành hai góc nhỏ có độ lớn bằng nhau. Nếu gọi góc ban đầu là $widehat{ABC}$ với đỉnh B, tia phân giác của góc này sẽ là tia BD (D nằm trên miền trong của góc) sao cho $widehat{ABD} = widehat{DBC}$.

Tia phân giác có tính chất quan trọng là mọi điểm nằm trên tia phân giác của một góc đều cách đều hai cạnh tạo nên góc đó. Tính chất này rất hữu ích trong việc chứng minh các định lý và giải các bài toán liên quan đến khoảng cách.

Hình vẽ minh họa tia phân giác của một góc, chia góc thành hai phần bằng nhau.

Cách Nhận Biết và Vẽ Tia Phân Giác

Để nhận biết một tia có phải là tia phân giác của một góc hay không, ta chỉ cần đo độ lớn của hai góc nhỏ được tạo bởi tia đó và hai cạnh của góc ban đầu. Nếu hai góc nhỏ này bằng nhau, thì tia đó chính là tia phân giác.

Xem Thêm Bài Viết:

Cách vẽ tia phân giác của một góc:

Bước 1: Vẽ một góc bất kỳ, ví dụ góc $widehat{ABC}$ với đỉnh là B.
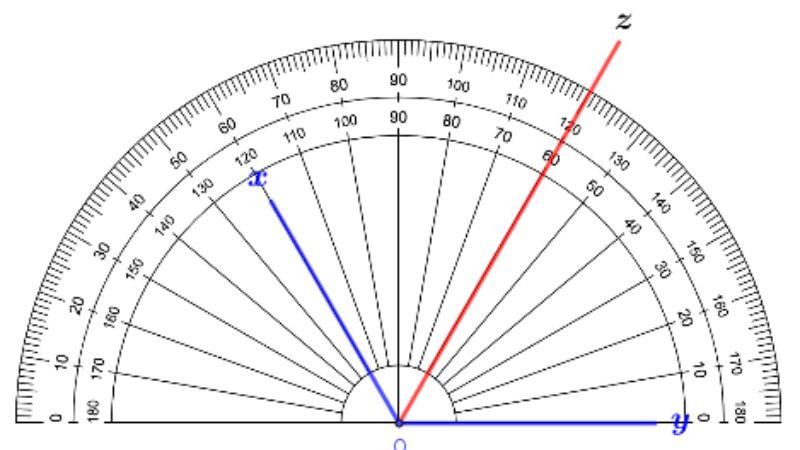
Bước 2: Đặt thước đo góc sao cho tâm của thước trùng với đỉnh B và cạnh 0 độ của thước trùng với một trong hai cạnh của góc (ví dụ BA). Đo độ lớn của góc $widehat{ABC}$.
Bước 3: Chia đôi độ lớn của góc $widehat{ABC}$ để xác định độ lớn của mỗi góc nhỏ mà tia phân giác sẽ tạo ra.
Bước 4: Đặt lại thước đo góc tại đỉnh B, đánh dấu một điểm D nằm trong góc sao cho góc $widehat{ABD}$ có độ lớn bằng một nửa độ lớn của góc $widehat{ABC}$ vừa tính ở Bước 3.
Bước 5: Kẻ tia BD từ đỉnh B đi qua điểm D vừa đánh dấu. Tia BD chính là tia phân giác của góc $widehat{ABC}$.

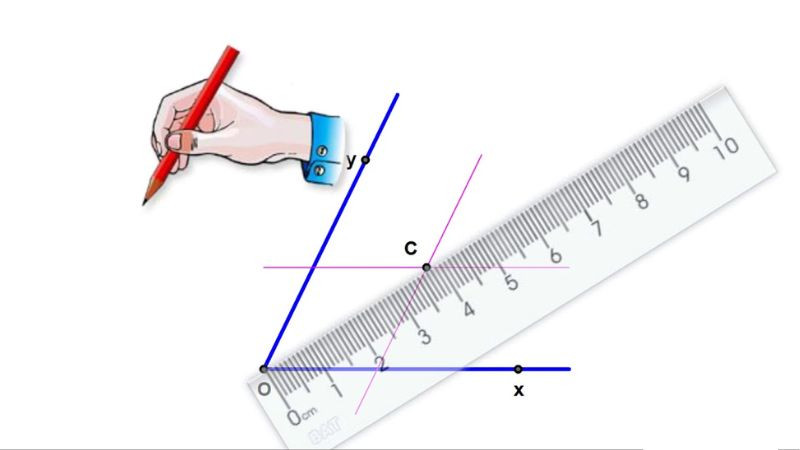Minh họa cách sử dụng thước đo góc để xác định tia phân giác.

Ngoài ra, có thể sử dụng compa và thước thẳng để vẽ tia phân giác một cách chính xác mà không cần đo độ.

Đường Phân Giác Trong Tam Giác Là Gì?

Trong phạm vi của một tam giác, đường phân giác là một đoạn thẳng nối từ một đỉnh của tam giác tới một điểm trên cạnh đối diện, và đoạn thẳng này nằm trên tia phân giác của góc tại đỉnh đó. Ví dụ, trong tam giác ABC, nếu AD là đường phân giác xuất phát từ đỉnh A (D nằm trên cạnh BC), thì tia AD là tia phân giác của góc $widehat{BAC}$.

Đường phân giác trong tam giác không chỉ chia đôi góc tại đỉnh mà còn có một tính chất đặc biệt liên quan đến tỷ lệ các cạnh. Định lý đường phân giác phát biểu rằng đường phân giác của một góc trong tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Hình vẽ minh họa đường phân giác trong một tam giác, nối đỉnh với cạnh đối diện.

Tính Chất Nổi Bật Của Tia và Đường Phân Giác

Tia và đường phân giác sở hữu những tính chất cốt lõi giúp giải quyết nhiều vấn đề trong hình học:

Chia Góc Thành Hai Phần Bằng Nhau: Đây là tính chất định nghĩa của tia phân giác. Bất kỳ tia nào được gọi là tia phân giác đều phải chia góc ban đầu thành hai góc nhỏ có độ lớn bằng nhau. Tính chất này là nền tảng cho nhiều chứng minh và tính toán liên quan đến góc trong tam giác và đa giác.

Minh họa tính chất chia góc thành hai phần bằng nhau của tia phân giác.

Tính Tỷ Lệ Cạnh Đối Diện (Đối với Đường Phân Giác trong Tam Giác): Nếu đường phân giác AD của tam giác ABC cắt cạnh BC tại D, thì ta có tỷ lệ: $frac{BD}{DC} = frac{AB}{AC}$. Tính chất này (Định lý đường phân giác) là một công cụ mạnh mẽ để tính độ dài các đoạn thẳng trên cạnh đối diện hoặc suy ra mối quan hệ giữa các cạnh trong tam giác.
Điểm Giao Nhau Của Các Đường Phân Giác (Tâm Đường Tròn Nội Tiếp): Trong một tam giác, ba đường phân giác xuất phát từ ba đỉnh sẽ đồng quy tại một điểm duy nhất. Điểm này được gọi là tâm đường tròn nội tiếp của tam giác. Từ tâm này, ta có thể vẽ một đường tròn tiếp xúc với cả ba cạnh của tam giác. Đây là một tính chất đặc biệt quan trọng trong các bài toán liên quan đến đường tròn và tam giác.

Ứng Dụng Tính Chất Của Tia và Đường Phân Giác

Các tính chất của tia và đường phân giác có ứng dụng rộng rãi trong nhiều lĩnh vực:

Chứng Minh Định Lý và Giải Bài Toán Hình Học: Các tính chất về chia đôi góc, tỷ lệ cạnh và điểm đồng quy là nền tảng để chứng minh nhiều định lý phức tạp hơn trong hình học tam giác. Chúng cũng là công cụ không thể thiếu để giải các bài toán tính toán liên quan đến độ dài, góc và vị trí tương đối của các điểm trong tam giác.

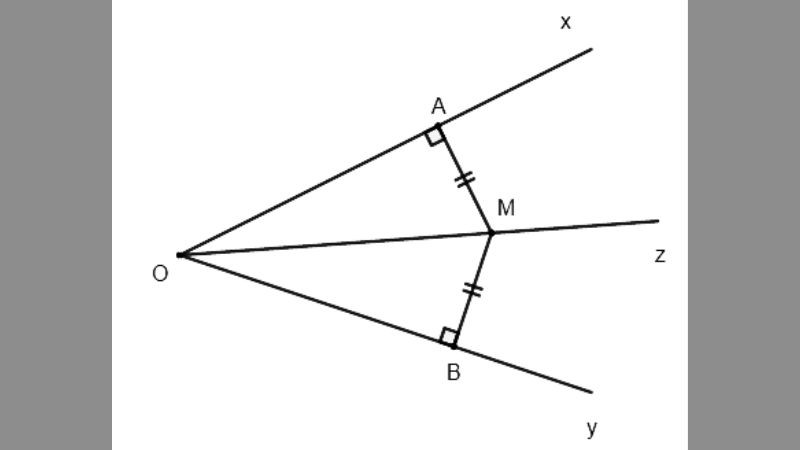Hình tam giác với đường phân giác minh họa tỷ lệ chia cạnh đối diện.

Thiết Kế Kiến Trúc và Kỹ Thuật: Trong kiến trúc, việc áp dụng các nguyên lý hình học, bao gồm cả tia phân giác, giúp tạo ra sự cân đối và hài hòa cho công trình. Trong kỹ thuật, đặc biệt là cơ khí chính xác, việc phân chia góc đều hoặc xác định tâm đối xứng dựa trên tia phân giác đảm bảo độ chính xác trong thiết kế và lắp ráp.

Phân Biệt Tia Phân Giác và Đường Phân Giác

Mặc dù có liên quan chặt chẽ, tia phân giác và đường phân giác là hai khái niệm khác nhau:

Tia Phân Giác: Là một tia (một phần của đường thẳng kéo dài vô hạn về một phía) bắt đầu từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Nó chỉ xác định hướng và vị trí chia đôi góc.

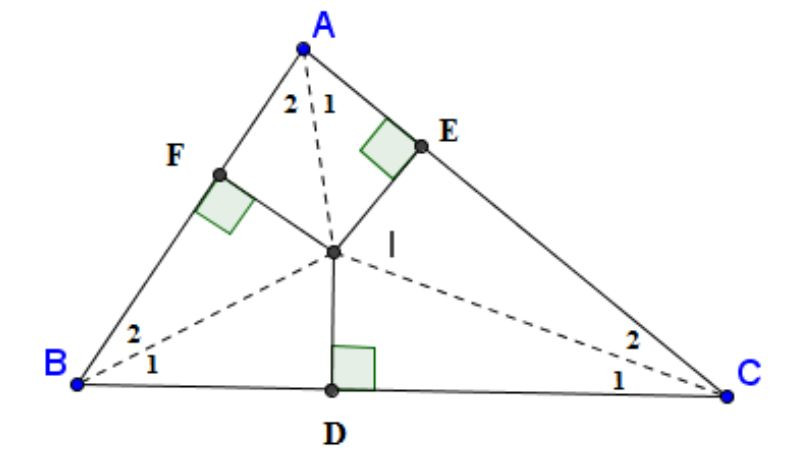Sơ đồ phân biệt tia phân giác (tia) và đường phân giác (đoạn thẳng trong tam giác).

Đường Phân Giác: Là một đoạn thẳng cụ thể trong một tam giác, nối một đỉnh với một điểm trên cạnh đối diện, và đoạn thẳng này nằm trên tia phân giác của góc tại đỉnh đó. Đường phân giác có độ dài xác định và chia cạnh đối diện theo một tỷ lệ nhất định.

Mối quan hệ: Đường phân giác trong tam giác chính là đoạn thẳng giới hạn của tia phân giác khi nó cắt cạnh đối diện của tam giác. Tia phân giác là khái niệm tổng quát cho một góc bất kỳ, còn đường phân giác là khái niệm áp dụng trong bối cảnh tam giác.

Ứng Dụng Thực Tiễn Của Tia Phân Giác

Tia phân giác không chỉ dừng lại ở lý thuyết hình học mà còn có nhiều ứng dụng thiết thực trong cuộc sống:

Trong Toán Học và Hình Học

Ngoài việc chứng minh định lý và giải bài toán cơ bản, tia phân giác còn giúp:

Xác định vị trí của tâm đường tròn nội tiếp, từ đó tính bán kính đường tròn nội tiếp và giải các bài toán liên quan đến diện tích tam giác.
Giải các bài toán về quỹ tích điểm, nơi các điểm có tính chất cách đều hai đường thẳng (tức là nằm trên tia phân giác của góc tạo bởi hai đường thẳng đó).
Chứng minh các tính chất đối xứng trong các hình phức tạp.

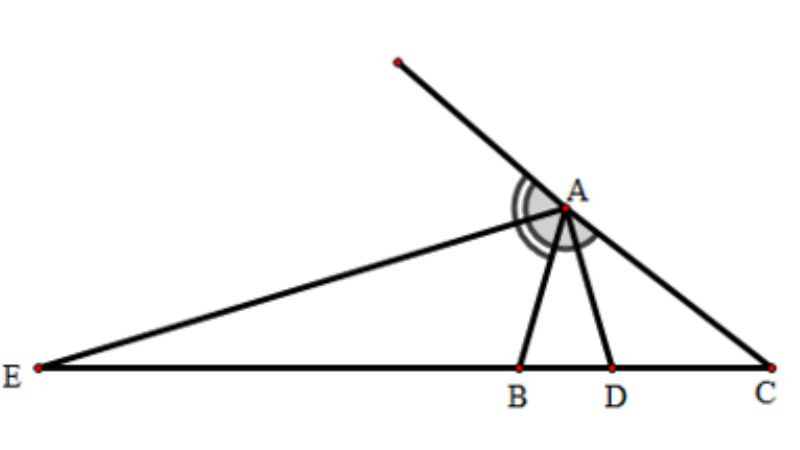Minh họa ứng dụng tia phân giác trong giải các bài toán hình học về góc và tam giác.

Trong Kiến Trúc và Kỹ Thuật

Thiết kế kiến trúc: Sử dụng tia phân giác để tạo ra các mặt bằng, mặt đứng hoặc chi tiết trang trí có tính đối xứng hoàn hảo, mang lại cảm giác cân bằng và thẩm mỹ.
Kỹ thuật cơ khí: Áp dụng để thiết kế các khớp nối, bánh răng, hoặc các bộ phận máy cần sự phân chia góc chính xác để đảm bảo hoạt động trơn tru và hiệu quả. Việc xác định đường tâm đối xứng thường liên quan đến khái niệm tia phân giác.

Ứng dụng của tia phân giác trong thiết kế kỹ thuật, đảm bảo tính chính xác và đối xứng.

Trong Đời Sống Hàng Ngày

Thiết kế nội thất: Bố trí đồ đạc, treo tranh ảnh hoặc sắp xếp không gian sao cho các yếu tố được cân đối và hài hòa, thường tuân theo nguyên tắc đối xứng ngầm hoặc rõ ràng, có liên quan đến việc chia đôi không gian hoặc góc nhìn.
Thiết kế đồ họa và nghệ thuật: Tạo ra các bố cục cân bằng, logo hoặc biểu tượng có tính đối xứng cao, thu hút thị giác. Nhiều họa sĩ và nhà thiết kế sử dụng các đường phân giác (dù là trực giác hay có tính toán) để định vị các yếu tố chính trong tác phẩm.
Giáo dục: Là một trong những khái niệm hình học cơ bản được dạy từ cấp phổ thông, giúp học sinh phát triển tư duy logic và khả năng phân tích không gian.

Tia phân giác giúp tạo ra sự cân đối và hài hòa trong trang trí nội thất.

Câu Hỏi Thường Gặp (FAQ) Về Tia Phân Giác

Làm thế nào để kiểm tra đường phân giác có chính xác không?
Để kiểm tra tính chính xác, bạn có thể đo độ lớn của hai góc nhỏ được tạo thành. Nếu chúng bằng nhau, tia đó là tia phân giác. Đối với đường phân giác trong tam giác, bạn có thể đo độ dài các đoạn trên cạnh đối diện và hai cạnh kề để kiểm tra tỷ lệ theo định lý đường phân giác.
Tại sao việc hiểu về tia và đường phân giác lại quan trọng?
Nắm vững khái niệm và tính chất của tia và đường phân giác là nền tảng để giải quyết các bài toán hình học về góc, tam giác và đường tròn nội tiếp. Nó còn mở rộng khả năng ứng dụng toán học vào các lĩnh vực thực tế như thiết kế, kỹ thuật, mang lại khả năng tư duy logic và phân tích không gian tốt hơn.
Những công cụ nào có thể giúp vẽ đường phân giác chính xác?
Các công cụ truyền thống bao gồm thước đo góc (để đo và đánh dấu) và compa kết hợp thước thẳng (để dựng hình không cần đo độ). Trong môi trường kỹ thuật số, các phần mềm vẽ hình học chuyên dụng như GeoGebra, AutoCAD cung cấp công cụ vẽ tia phân giác nhanh chóng và chính xác.
Đường phân giác có ảnh hưởng đến các thuộc tính khác của tam giác không?
Có, đường phân giác ảnh hưởng đến nhiều thuộc tính của tam giác. Nó xác định vị trí của tâm đường tròn nội tiếp, liên quan trực tiếp đến tỷ lệ độ dài các đoạn trên cạnh đối diện, và gián tiếp ảnh hưởng đến các tính toán về diện tích, chu vi, và các điểm đặc biệt khác trong tam giác.

Lời Kết

Tia phân giác và đường phân giác là những khái niệm cơ bản nhưng đóng vai trò thiết yếu trong hình học và có sức ảnh hưởng rộng rãi trong nhiều lĩnh vực của đời sống. Từ việc chia đôi một góc đơn giản đến việc xác định tâm đường tròn nội tiếp hay tạo ra những thiết kế kiến trúc cân đối, vai trò của chúng là không thể phủ nhận.

Bài viết này đã cung cấp một cái nhìn chi tiết về định nghĩa, cách xác định, các tính chất quan trọng và ứng dụng đa dạng của tia và đường phân giác. Hy vọng rằng thông tin này giúp bạn không chỉ hiểu rõ hơn về các khái niệm hình học này mà còn thấy được giá trị ứng dụng thực tế của chúng. Để thực sự thành thạo, việc luyện tập vẽ và áp dụng các tính chất vào giải các bài toán cụ thể là vô cùng quan trọng.