Số nguyên tố là một khái niệm cơ bản và quan trọng trong toán học, đặc biệt là lý thuyết số. Chúng là nền tảng để xây dựng nên các số tự nhiên lớn hơn thông qua phép nhân. Vậy chính xác số nguyên tố là gì và chúng có những đặc điểm, ứng dụng nào? Bài viết này sẽ giải đáp chi tiết cho bạn.
Định Nghĩa Số Nguyên Tố Và Ví Dụ Minh Họa
Theo định nghĩa toán học, số nguyên tố là các số tự nhiên lớn hơn 1, chỉ có đúng hai ước số dương phân biệt là 1 và chính nó. Nói cách khác, một số tự nhiên N (với N > 1) được gọi là số nguyên tố nếu N không chia hết cho bất kỳ số tự nhiên nào khác ngoài 1 và N.
Ngược lại với số nguyên tố là hợp số. Hợp số là các số tự nhiên lớn hơn 1 có nhiều hơn hai ước số dương. Số 1 không phải là số nguyên tố cũng không phải là hợp số.
Ví dụ điển hình về số nguyên tố bao gồm: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 997…
Hình ảnh minh họa định nghĩa số nguyên tố là các số tự nhiên lớn hơn 1 chỉ chia hết cho 1 và chính nó
- Vẽ tranh trò chơi dân gian kéo co: Tái hiện sinh động
- Game Booster Là Gì? Tối Ưu Hiệu Năng Chơi Game Trên Điện Thoại Di Động
- Sắc màu và ý nghĩa: Nước tiểu bình thường có màu gì?
- Khám Phá Cách Vẽ Váy Đơn Giản Cho Người Mới Bắt Đầu
- Nơi Học Mỹ Thuật Ở Đâu: Hành Trình Tìm Kiếm Không Gian Sáng Tạo
Các Tính Chất Đặc Trưng Của Số Nguyên Tố
Số nguyên tố sở hữu những tính chất riêng biệt và thú vị, là chìa khóa để hiểu sâu hơn về cấu trúc của tập hợp số tự nhiên. Nắm vững các tính chất này sẽ giúp bạn dễ dàng nhận biết và làm việc với số nguyên tố.
- Số nguyên tố chẵn duy nhất: Số 2 là số nguyên tố chẵn duy nhất. Tất cả các số nguyên tố lớn hơn 2 đều là số lẻ. Số 2 cũng là số nguyên tố nhỏ nhất trong dãy số tự nhiên.
- Ước số nhỏ nhất khác 1: Mọi số tự nhiên lớn hơn 1 đều có ít nhất một ước số nguyên tố. Ước số dương nhỏ nhất khác 1 của một số tự nhiên bất kỳ (lớn hơn 1) luôn là một số nguyên tố.
- Tính vô hạn: Tập hợp các số nguyên tố là vô hạn. Điều này đã được chứng minh từ thời Euclid và là một kết quả kinh điển trong lý thuyết số, khẳng định rằng không có số nguyên tố lớn nhất.
- Tích của hai số nguyên tố: Tích của hai số nguyên tố khác nhau không thể là một số chính phương. Ví dụ, 3 5 = 15 (không chính phương). Tuy nhiên, tích của một số nguyên tố với chính nó (bình phương của số nguyên tố) lại là một số chính phương (ví dụ: 3 3 = 9, là chính phương).
- Tiêu chí kiểm tra tính nguyên tố (đến căn bậc hai): Nếu một số tự nhiên N (N > 1) không có bất kỳ ước số nguyên tố nào nhỏ hơn hoặc bằng căn bậc hai của N (√N), thì N là số nguyên tố. Đây là cơ sở cho nhiều thuật toán kiểm tra tính nguyên tố hiệu quả.
Số 2 là số nguyên tố chẵn duy nhất, số nguyên tố nhỏ nhất trong dãy số tự nhiên
Các Phương Pháp Tìm Kiếm Và Kiểm Tra Số Nguyên Tố
Việc xác định một số có phải là số nguyên tố hay không, hoặc tìm ra các số nguyên tố trong một khoảng nhất định là những bài toán thường gặp. Dưới đây là một số phương pháp phổ biến.
-
Phương pháp thử phép chia (Trial Division):
Để kiểm tra xem số tự nhiên N (N > 1) có phải là số nguyên tố hay không, ta thực hiện phép chia N cho tất cả các số tự nhiên từ 2 lên đến một giới hạn nhất định.- Cách cơ bản: Thử chia N cho các số từ 2 đến N-1. Nếu N chia hết cho bất kỳ số nào trong khoảng này, thì N là hợp số. Nếu không chia hết cho số nào, N là số nguyên tố. Phương pháp này đơn giản nhưng kém hiệu quả với số lớn.
- Cách hiệu quả hơn (dựa trên căn bậc hai): Chỉ cần kiểm tra xem N có chia hết cho bất kỳ số nguyên tố nào nhỏ hơn hoặc bằng căn bậc hai của N (√N) hay không. Nếu không có ước số nguyên tố nào trong phạm vi này, thì N là số nguyên tố. Ví dụ: Kiểm tra số 101. √101 ≈ 10.05. Các số nguyên tố cần kiểm tra là 2, 3, 5, 7. 101 không chia hết cho 2, 3, 5, 7. Do đó, 101 là số nguyên tố.
-
Sử dụng máy tính bỏ túi:
Một số máy tính bỏ túi hiện đại có chức năng kiểm tra tính nguyên tố hoặc phân tích thừa số nguyên tố. Thông thường, bạn nhập số cần kiểm tra, sau đó sử dụng chức năng phân tích thừa số (thường là phím ‘FACT’ hoặc tương tự). Nếu máy tính hiển thị lại chính số đó, nghĩa là nó là số nguyên tố. Nếu hiển thị dưới dạng tích của các số khác, đó là hợp số. -
Sàng Eratosthenes (để tìm nhiều số nguyên tố trong một khoảng):
Đây là một thuật toán hiệu quả để tìm tất cả các số nguyên tố trong một phạm vi nhất định (ví dụ: dưới 100, dưới 1000…). Quy trình đơn giản như sau:- Liệt kê tất cả các số tự nhiên từ 2 đến giới hạn N.
- Bắt đầu với số nguyên tố đầu tiên là 2. Gạch bỏ tất cả các bội số của 2 (4, 6, 8,…).
- Tìm số chưa bị gạch nhỏ nhất tiếp theo (đó là 3). Gạch bỏ tất cả các bội số của 3 (6, 9, 12,…).
- Lặp lại quy trình này với số chưa bị gạch nhỏ nhất tiếp theo cho đến khi bạn đạt đến căn bậc hai của N (√N).
- Các số còn lại trong danh sách (chưa bị gạch) chính là các số nguyên tố nhỏ hơn hoặc bằng N.
Bảng Số Nguyên Tố Nhỏ Hơn 100
Để tiện tra cứu và làm quen, dưới đây là danh sách tất cả các số nguyên tố trong phạm vi dưới 100 được tìm thấy bằng các phương pháp trên:
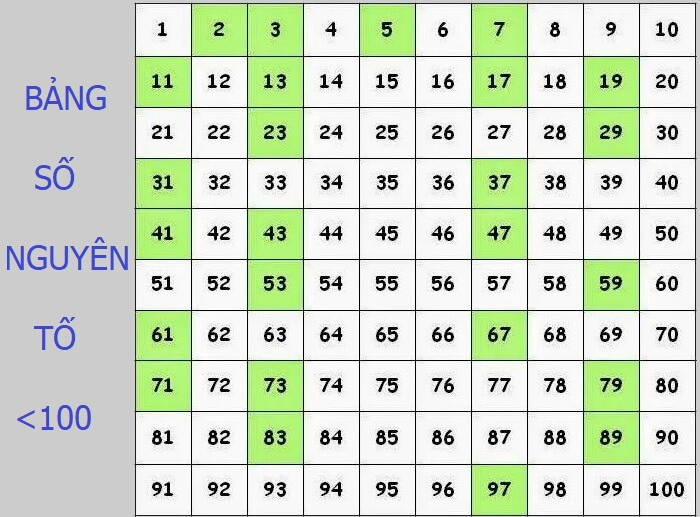Bảng liệt kê các số nguyên tố nhỏ hơn 100 giúp tra cứu và nhận biết nhanh chóng
Các số nguyên tố nhỏ hơn 100 là: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Các Khái Niệm Liên Quan Đến Số Nguyên Tố
Thế giới của số nguyên tố còn liên kết với nhiều khái niệm thú vị khác trong toán học.
Số nguyên tố cùng nhau (Coprime Numbers)
Hai số tự nhiên a và b được gọi là số nguyên tố cùng nhau nếu ước chung lớn nhất (ƯCLN) của chúng bằng 1. Điều này không có nghĩa là bản thân a và b phải là số nguyên tố. Ví dụ: Số 8 và số 15 là số nguyên tố cùng nhau vì ƯCLN(8, 15) = 1 (Ước của 8 là 1, 2, 4, 8; Ước của 15 là 1, 3, 5, 15. Ước chung duy nhất là 1). Số 5 và 23 cũng là số nguyên tố cùng nhau, vì 5 và 23 đều là số nguyên tố nên ƯCLN của chúng là 1.
Số siêu nguyên tố (Superprime / Truncatable Prime / Emirp)
Thuật ngữ “số siêu nguyên tố” đôi khi được sử dụng để chỉ các số nguyên tố có những tính chất đặc biệt liên quan đến các chữ số của nó. Có nhiều định nghĩa khác nhau cho khái niệm này trong các ngữ cảnh khác nhau.
- Số nguyên tố cắt cụt (Truncatable Prime): Là số nguyên tố mà khi bỏ một hoặc nhiều chữ số ở đầu (Left-truncatable prime) hoặc cuối (Right-truncatable prime) vẫn tạo thành các số nguyên tố. Ví dụ, 313 là số nguyên tố cắt cụt phải (313 -> 31 -> 3, tất cả đều là số nguyên tố).
- Emirp (Prime ngược lại): Là số nguyên tố mà khi đảo ngược thứ tự các chữ số cũng tạo thành một số nguyên tố khác. Ví dụ: 13 là nguyên tố, đảo ngược là 31 cũng là nguyên tố; 1337 là nguyên tố, đảo ngược là 7331 cũng là nguyên tố.
Phân tích một số ra thừa số nguyên tố (Prime Factorization)
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là việc biểu diễn số đó dưới dạng tích của các số nguyên tố. Cách phân tích này là duy nhất cho mỗi số (chỉ khác nhau về thứ tự các thừa số) và là một công cụ mạnh mẽ trong nhiều bài toán toán học (tìm ƯCLN, BCNN, rút gọn phân số…).
Ví dụ:
- 6 = 2 * 3 (2 và 3 là các thừa số nguyên tố của 6)
- 105 = 3 5 7 (3, 5, 7 là các thừa số nguyên tố của 105)
- 12 = 2 2 3 = 2² * 3 (2 và 3 là các thừa số nguyên tố của 12)
Số nguyên tố không chỉ là một chủ đề hấp dẫn trong toán học thuần túy mà còn có ứng dụng rộng rãi trong mật mã học, khoa học máy tính và nhiều lĩnh vực khác. Hiểu rõ về số nguyên tố giúp chúng ta nắm bắt được những nền tảng cơ bản về cấu trúc của số học.
