Thừa số là một khái niệm cơ bản trong toán học, đặc biệt liên quan đến phép nhân. Chúng là các số hoặc biểu thức được nhân với nhau để tạo ra một số hoặc biểu thức khác, gọi là tích. Hiểu rõ về thừa số giúp chúng ta nắm vững bản chất của phép nhân, phân tích cấu trúc của các con số và ứng dụng trong nhiều lĩnh vực toán học nâng cao như đại số hay lý thuyết số.
Tìm hiểu về thừa số là gì?
Trong phép nhân, các số được nhân với nhau được gọi là thừa số, và kết quả của phép nhân được gọi là tích. Khái niệm này rất quan trọng để hiểu cấu trúc của phép nhân và mối quan hệ giữa các số.
Ví dụ: Trong phép tính 2 x 6 = 12, số 2 và số 6 là các thừa số, còn số 12 là tích.
Biểu diễn phép nhân a x b = c, làm rõ thừa số và tích
Trong các phép toán khác, các thành phần cũng có tên gọi riêng: số hạng trong phép cộng, số bị trừ và số trừ trong phép trừ, số bị chia và số chia trong phép chia. Việc gọi tên các thành phần trong phép toán giúp chúng ta nhận biết vai trò và ý nghĩa của từng con số, từ đó hiểu sâu hơn về tính chất của phép toán đó.
Xem Thêm Bài Viết:- **6/33 Là Màu Gì**: Tông Vàng Kim Đậm Ấm Áp
- Google Hangout Là Gì? Hướng Dẫn Sử Dụng Chi Tiết Từ A-Z
- Tuyển Tập Tranh Tô Màu Hello Kitty Theo Độ Tuổi: Hướng Dẫn Chọn Mẫu Phù Hợp Cho Bé
- Áo Màu Tím Phối Với Quần Màu Gì Sành Điệu Nhất
- Chiêm ngưỡng ảnh phong cảnh buồn đầy cảm xúc
Tìm hiểu về thừa số nguyên tố
Thừa số nguyên tố là một khái niệm đặc biệt liên quan đến các số nguyên tố. Mọi số tự nhiên lớn hơn 1 đều có thể được phân tích thành tích của các số nguyên tố. Các số nguyên tố trong tích đó chính là thừa số nguyên tố của số tự nhiên ban đầu.
Để hiểu rõ hơn, ta cần nắm vững:
- Số nguyên tố: Là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Các số như 2, 3, 5, 7, 11… là số nguyên tố.
- Phân tích thừa số nguyên tố: Là quá trình tách một số tự nhiên lớn hơn 1 thành tích của các thừa số chỉ là số nguyên tố. Quá trình này dừng lại khi tất cả các thừa số cuối cùng đều là số nguyên tố.
Sơ đồ minh họa quá trình phân tích số 48 thành thừa số nguyên tố
Ví dụ: Phân tích số 48 thành thừa số nguyên tố.
Ta lần lượt chia 48 cho các số nguyên tố nhỏ nhất có thể chia hết:
- 48 : 2 = 24
- 24 : 2 = 12
- 12 : 2 = 6
- 6 : 2 = 3
Số 3 là số nguyên tố, nên ta dừng lại.
Như vậy, 48 = 2 x 2 x 2 x 2 x 3. Các thừa số nguyên tố của 48 là 2 (xuất hiện 4 lần) và 3 (xuất hiện 1 lần).
Cách phân tích một số tự nhiên thành thừa số nguyên tố
Có nhiều cách để phân tích một số thành thừa số. Một trong những phương pháp phổ biến và có hệ thống nhất là sử dụng phép chia cho các số nguyên tố.
Đầu tiên, tìm các thừa số (ước số) của số cần phân tích. Một thừa số của một số là số mà số đó chia hết cho nó mà không có số dư.
Tìm các thừa số (ước số) của một số tự nhiên cụ thể
Phương pháp phân tích thành thừa số nguyên tố bằng cách chia:
- Viết số cần phân tích ở bên trái một đường kẻ dọc.
- Tìm số nguyên tố nhỏ nhất có thể chia hết cho số ở bên trái. Viết số nguyên tố này ở bên phải đường kẻ.
- Thực hiện phép chia. Viết kết quả (thương) ở bên dưới số ban đầu, cùng cột bên trái.
- Tiếp tục quá trình này với số thương mới. Lặp lại bước 2 và 3 cho đến khi số ở cột bên trái là 1.
- Các số nguyên tố ở cột bên phải chính là các thừa số nguyên tố của số ban đầu.
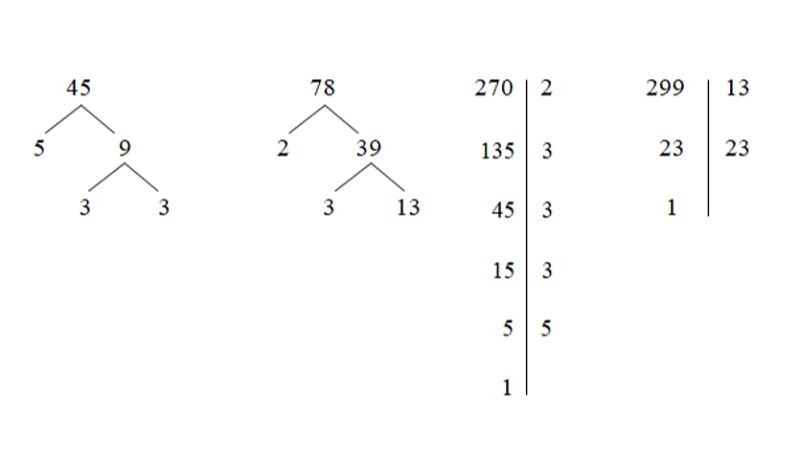Sơ đồ chia dọc minh họa phương pháp phân tích một số thành thừa số nguyên tố
Ví dụ áp dụng lại với số 48:
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1 |Các thừa số nguyên tố là các số ở cột bên phải: 2, 2, 2, 2, 3.
Ý nghĩa của việc tìm thừa số
Việc tìm ra các thừa số của một số, đặc biệt là phân tích thành thừa số nguyên tố, đóng vai trò cực kỳ quan trọng trong toán học. Nó không chỉ giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của các con số mà còn là nền tảng cho nhiều khái niệm và kỹ thuật toán học phức tạp hơn.
Minh họa trừu tượng về tầm quan trọng của việc phân tích thừa số trong các vấn đề toán học
Phân tích thừa số cho phép ta:
- Xác định tất cả các ước số (hay thừa số) của một số.
- Tìm ước số chung lớn nhất (ƯCLN) và bội số chung nhỏ nhất (BCNN) của hai hay nhiều số, rất hữu ích trong việc rút gọn phân số và giải các bài toán liên quan đến chia hết.
- Hiểu rõ tính chất chia hết của các số.
- Làm quen với tư duy phân tách vấn đề lớn thành các phần nhỏ hơn, đơn giản hơn, một kỹ năng quan trọng trong giải toán và nhiều lĩnh vực khác.
- Là cơ sở cho các chủ đề toán học cao cấp hơn như đại số (phân tích đa thức thành nhân tử) và lý thuyết số.
Quá trình phân tích thừa số có thể coi là “phép nhân ngược”, giúp rèn luyện khả năng nhìn nhận vấn đề từ nhiều góc độ.
Lưu ý khi phân tích thừa số nguyên tố
Để thực hiện việc phân tích thừa số nguyên tố một cách chính xác và hiệu quả, cần lưu ý một số điểm sau:
- Hiểu rõ khái niệm: Nắm vững định nghĩa thừa số là gì và đặc biệt là số nguyên tố. Thừa số nguyên tố phải là số nguyên tố.
- Bắt đầu với số nguyên tố nhỏ nhất: Luôn ưu tiên chia cho các số nguyên tố nhỏ như 2, 3, 5, 7 trước khi thử các số lớn hơn. Điều này giúp quá trình phân tích có hệ thống và dễ dàng hơn.
- Chỉ xét số dương: Khi phân tích một số, ta thường xét với giá trị tuyệt đối của nó.
- Ghi chép cẩn thận: Ghi lại các bước chia và các thừa số nguyên tố tìm được để không bỏ sót bất kỳ thừa số nào.
- Kiểm tra lại kết quả: Sau khi hoàn thành, nhân tất cả các thừa số nguyên tố tìm được với nhau để kiểm tra xem tích có bằng số ban đầu hay không.
- Thường xuyên luyện tập: Phân tích thừa số là một kỹ năng, cần luyện tập thường xuyên với nhiều dạng số khác nhau để thành thạo.
Danh sách kiểm tra các lưu ý cần nhớ khi phân tích một số thành thừa số nguyên tố
Một số dạng bài tập phổ biến về thừa số, tích và phép nhân
Trong chương trình học, có một số dạng bài tập cơ bản liên quan đến thừa số, tích và phép nhân:
Dạng 1: Tìm giá trị của tích
Đây là dạng bài tập cơ bản nhất của phép nhân, yêu cầu tìm kết quả khi biết các thừa số. Có thể hình dung phép nhân như phép cộng lặp lại để dễ hiểu.
Ví dụ về bài toán xác định giá trị của tích từ các thừa số đã cho
Ví dụ: Tìm tích của 3 và 5.
Ta có phép nhân 3 x 5. Đây có thể hiểu là cộng số 5 lại 3 lần: 5 + 5 + 5 = 15.
Vậy, 3 x 5 = 15.
Trong đó, 3 và 5 là thừa số, 15 là tích.
Dạng 2: Tìm giá trị của thừa số hoặc tích trong phép tính nhân
Dạng này yêu cầu xác định vai trò (thừa số hay tích) hoặc tìm giá trị còn thiếu trong một phép nhân.
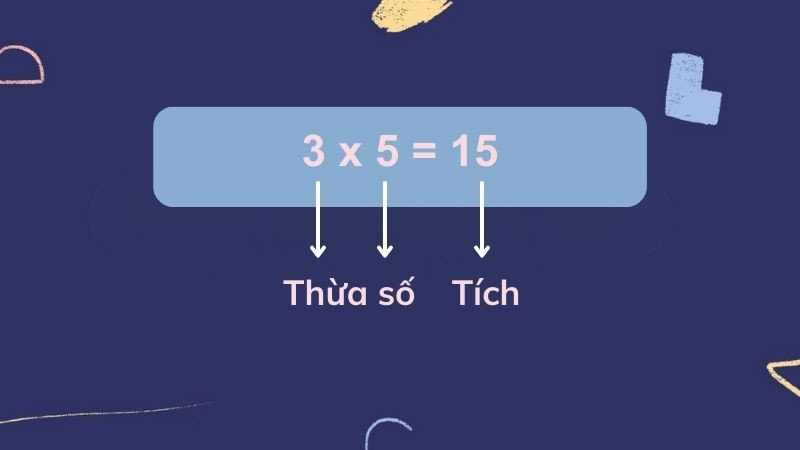Hình ảnh làm rõ vị trí và tên gọi của thừa số và tích trong phép nhân
Ví dụ:
- Xác định thừa số và tích trong phép tính 7 x 8 = 56.
Trả lời: 7 và 8 là thừa số, 56 là tích. - Tìm số còn thiếu: 4 x ? = 20.
Để tìm thừa số còn thiếu, ta lấy tích chia cho thừa số đã biết: 20 : 4 = 5.
Vậy, 4 x 5 = 20. Thừa số còn thiếu là 5.
Dạng 3: Toán đố
Dạng toán có lời văn đòi hỏi khả năng đọc hiểu, phân tích đề bài và vận dụng kiến thức về thừa số, tích, phép nhân (và đôi khi cả phân tích thừa số nguyên tố) để giải quyết vấn đề thực tế.
Hình ảnh bài toán đố về việc phân chia đối tượng thành các nhóm bằng nhau, sử dụng khái niệm thừa số
Ví dụ: Lan có 24 viên kẹo, Lan muốn chia đều số kẹo này vào các túi sao cho mỗi túi có cùng số lượng kẹo. Hỏi có những cách nào để Lan chia số kẹo đó?
Lời giải: Bài toán yêu cầu tìm các cách chia đều 24 viên kẹo, tức là tìm các cặp thừa số của 24.
Ta cần tìm các số tự nhiên a và b sao cho a x b = 24.
Các cặp thừa số của 24 là:
1 x 24 = 24
2 x 12 = 24
3 x 8 = 24
4 x 6 = 24
6 x 4 = 24
8 x 3 = 24
12 x 2 = 24
24 x 1 = 24
Vậy, Lan có thể chia kẹo theo các cách sau: 1 túi (24 viên), 2 túi (12 viên/túi), 3 túi (8 viên/túi), 4 túi (6 viên/túi), 6 túi (4 viên/túi), 8 túi (3 viên/túi), 12 túi (2 viên/túi), hoặc 24 túi (1 viên/túi).
Tóm lại, thừa số là một khái niệm nền tảng trong toán học, đặc biệt là phép nhân. Việc hiểu và biết cách phân tích một số thành các thừa số, đặc biệt là thừa số nguyên tố, không chỉ củng cố kiến thức cơ bản mà còn mở ra cánh cửa đến với nhiều lĩnh vực toán học phức tạp hơn. Nắm vững kỹ năng này là bước đệm quan trọng để giải quyết các bài toán liên quan đến ƯCLN, BCNN, rút gọn phân số và các vấn đề đại số.
