Trong lĩnh vực hình học, trọng tâm là một khái niệm nền tảng và mang nhiều ý nghĩa. Nó không chỉ đơn thuần là một điểm trong tam giác mà còn nắm giữ những tính chất đặc biệt, đóng vai trò quan trọng trong nhiều ứng dụng thực tế từ kiến trúc, kỹ thuật đến vật lý. Hiểu rõ về trọng tâm giúp chúng ta có cái nhìn sâu sắc hơn về cấu trúc và cân bằng của các hình phẳng. Vậy, thực chất trọng tâm của tam giác là gì, có những tính chất nổi bật nào và làm thế nào để xác định chính xác vị trí của nó? Bài viết này sẽ cung cấp thông tin chi tiết để giải đáp những câu hỏi đó.
Trọng tâm là gì?
Trọng tâm của một tam giác là điểm đặc biệt nằm bên trong tam giác, được định nghĩa là giao điểm của ba đường trung tuyến. Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện đỉnh đó. Mỗi tam giác có ba đỉnh, tương ứng với ba đường trung tuyến. Ba đường trung tuyến này luôn đồng quy tại một điểm duy nhất, và điểm đó chính là trọng tâm của tam giác.
Hình ảnh minh họa trọng tâm tam giác là giao điểm của ba đường trung tuyến.
Điểm trọng tâm không chỉ quan trọng trong hình học phẳng mà còn có ý nghĩa vật lý sâu sắc. Nó đại diện cho điểm cân bằng khối lượng của một tấm phẳng đồng chất có hình dạng tam giác. Nếu bạn cắt một tam giác bằng vật liệu đồng nhất, bạn có thể cân bằng nó trên một đầu ngón tay đặt tại trọng tâm. Điều này cho thấy mối liên hệ giữa hình học thuần túy và các ứng dụng trong cơ học, kỹ thuật.
Ngoài ra, việc hiểu rõ khái niệm và tính chất của trọng tâm còn là chìa khóa để giải quyết nhiều bài toán hình học phức tạp hơn. Nếu bạn đang tìm hiểu sâu hơn về điểm đặc biệt này, hãy cùng khám phá những tính chất và cách xác định trọng tâm được trình bày chi tiết dưới đây.
Xem Thêm Bài Viết:- Khám Phá Màu Sắc Hợp Mệnh Năm Nay Hút Vận May
- Chi tiết nội dung chương trình lớp 1 hiện hành
- Cách Pha Màu Gấu Dâu Chuẩn Xác Cho Tranh Vẽ Của Bạn
- Công Nghệ Cấp Đông Mềm Trên Tủ Lạnh: Bảo Quản Tươi Ngon, Chế Biến Dễ Dàng
- Tuyển Chọn Ảnh Anime Nữ Cute Đáng Yêu Nhất
Tính chất của trọng tâm tam giác
Trọng tâm của tam giác sở hữu một số tính chất hình học nổi bật và quan trọng. Nắm vững các tính chất này giúp chúng ta dễ dàng hơn trong việc giải các bài tập và ứng dụng thực tế. Dưới đây là các tính chất cơ bản của trọng tâm G trong tam giác:
- Giao điểm của các đường trung tuyến: Theo định nghĩa, trọng tâm G là điểm chung duy nhất của ba đường trung tuyến trong tam giác.
- Chia đường trung tuyến theo tỷ lệ: Trọng tâm G chia mỗi đường trung tuyến thành hai đoạn thẳng theo tỷ lệ 2:1, tính từ đỉnh. Cụ thể, nếu AD là đường trung tuyến từ đỉnh A đến trung điểm D của cạnh BC, thì G nằm trên AD sao cho AG = (2/3) AD và GD = (1/3) AD. Tương tự cho hai đường trung tuyến còn lại.
- Điểm cân bằng khối lượng: Trọng tâm G là trung tâm khối lượng của tam giác. Đây là điểm mà tại đó, nếu tam giác là một vật thể đồng chất, nó có thể được cân bằng hoàn hảo.
Mô tả các tính chất cơ bản của trọng tâm G trong tam giác ABC, bao gồm tỷ lệ chia đường trung tuyến.
Các tính chất này là nền tảng cho nhiều bài toán và ứng dụng liên quan đến trọng tâm trong hình học và các lĩnh vực khoa học khác.
Trọng tâm của các loại tam giác đặc biệt
Vị trí và tính chất của trọng tâm có thể mang những đặc điểm riêng trong các loại tam giác đặc biệt như tam giác vuông, tam giác cân và tam giác đều.
Trọng tâm trong tam giác vuông
Trong tam giác vuông, trọng tâm vẫn là giao điểm của ba đường trung tuyến và chia mỗi đường theo tỷ lệ 2:1. Tuy nhiên, vị trí của nó có thể được xác định dễ dàng hơn nếu biết tọa độ các đỉnh. Nếu tam giác ABC vuông tại A, và M, N, P lần lượt là trung điểm của BC, AC, AB, thì các đường trung tuyến AM, BN, CP sẽ đồng quy tại trọng tâm G.
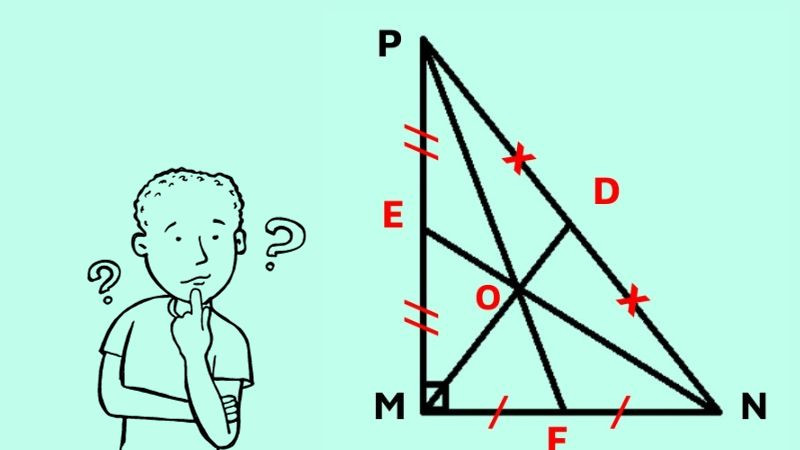Trọng tâm của tam giác vuông, minh họa vị trí đặc biệt của điểm G.
Một đặc điểm đáng chú ý là trung điểm M của cạnh huyền BC chính là tâm đường tròn ngoại tiếp tam giác vuông. Trọng tâm G nằm trên đường trung tuyến AM và cách A một khoảng bằng 2/3 độ dài AM. Độ dài đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền (AM = 1/2 BC). Do đó, AG = (2/3) * (1/2) BC = (1/3) BC. Vị trí trọng tâm trong tam giác vuông liên quan mật thiết đến các đỉnh và trung điểm cạnh huyền.
Trọng tâm trong tam giác cân
Trong tam giác cân, ví dụ tam giác ABC cân tại A (AB = AC), đường trung tuyến xuất phát từ đỉnh cân A (đường trung tuyến AM, với M là trung điểm BC) cũng đồng thời là đường cao, đường phân giác và đường trung trực của cạnh đáy BC. Do đó, trọng tâm G của tam giác cân nằm trên đường thẳng đặc biệt này – trục đối xứng của tam giác cân.
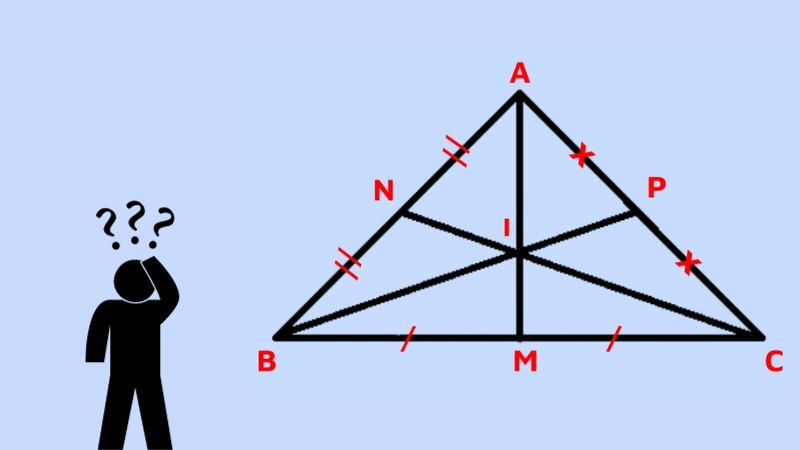Vị trí trọng tâm tam giác cân, nằm trên đường trung tuyến xuất phát từ đỉnh đối diện đáy.
Trọng tâm G chia đường trung tuyến AM theo tỷ lệ AG = (2/3) AM và GM = (1/3) AM. Việc trọng tâm nằm trên trục đối xứng giúp đơn giản hóa việc xác định vị trí của nó trong nhiều trường hợp.
Trọng tâm trong tam giác đều
Tam giác đều là trường hợp đặc biệt của tam giác cân, có ba cạnh bằng nhau và ba góc bằng 60 độ. Trong tam giác đều, ba đường trung tuyến có độ dài bằng nhau và mỗi đường trung tuyến đồng thời là đường cao, đường phân giác, và đường trung trực. Do đó, trọng tâm G của tam giác đều không chỉ là giao điểm của ba đường trung tuyến mà còn trùng với nhiều tâm đặc biệt khác của tam giác, bao gồm:
- Tâm đường tròn ngoại tiếp (circumcenter): Cách đều ba đỉnh.
- Tâm đường tròn nội tiếp (incenter): Cách đều ba cạnh.
- Trực tâm (orthocenter): Giao điểm của ba đường cao.
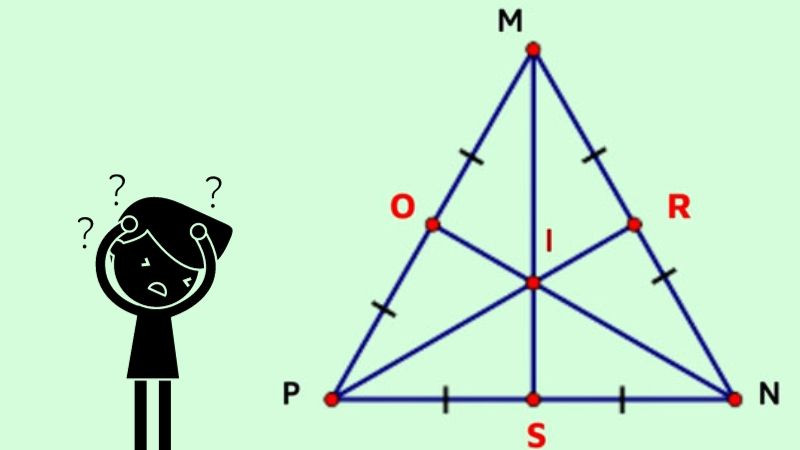Trọng tâm tam giác đều trùng với các tâm đặc biệt khác và là tâm đối xứng.
Trọng tâm G là tâm đối xứng quay của tam giác đều (đối xứng qua góc quay 120 độ). Vị trí trùng lặp của trọng tâm với các tâm khác trong tam giác đều làm cho nó trở thành một điểm trung tâm hoàn hảo, thể hiện sự cân đối tuyệt đối của hình dạng này.
Cách xác định chính xác trọng tâm trong tam giác
Có hai phương pháp chính để xác định trọng tâm của một tam giác: sử dụng công thức toán học (khi biết tọa độ các đỉnh) và sử dụng công cụ hình học (vẽ).
Cách 1: Sử dụng công thức toán học
Nếu biết tọa độ ba đỉnh của tam giác, việc xác định tọa độ trọng tâm trở nên rất đơn giản bằng cách sử dụng công thức trung bình cộng. Giả sử tam giác ABC có ba đỉnh là A(xA, yA), B(xB, yB) và C(xC, yC). Trọng tâm G(xG, yG) của tam giác sẽ có tọa độ được tính theo công thức:
xG = (xA + xB + xC) / 3
yG = (yA + yB + yC) / 3
Công thức tính tọa độ trọng tâm G của tam giác ABC dựa trên tọa độ các đỉnh.
Công thức này phản ánh tính chất trọng tâm là trung tâm khối lượng, nơi tọa độ của nó là trung bình của tọa độ các đỉnh, mỗi đỉnh được coi như có khối lượng bằng nhau. Phương pháp này đặc biệt hiệu quả trong hình học giải tích và các ứng dụng cần tính toán chính xác vị trí.
Ngoài ra, nếu không có tọa độ, bạn vẫn có thể xác định trọng tâm bằng cách sử dụng tính chất giao điểm của đường trung tuyến trong mặt phẳng tọa độ. Viết phương trình của ít nhất hai đường trung tuyến và giải hệ phương trình để tìm tọa độ giao điểm của chúng, chính là tọa độ trọng tâm G.
Cách 2: Sử dụng công cụ hình học
Phương pháp truyền thống để xác định trọng tâm là sử dụng thước kẻ và compa để vẽ hình trực tiếp. Cách thực hiện như sau:
- Xác định trung điểm của ít nhất hai cạnh của tam giác. Để tìm trung điểm của một cạnh, bạn có thể đo độ dài cạnh đó bằng thước và chia đôi, hoặc dùng compa để vẽ hai cung tròn với bán kính lớn hơn nửa cạnh từ hai đầu mút của cạnh đó; giao điểm của hai cung tròn này khi nối lại sẽ đi qua trung điểm.
- Vẽ đường trung tuyến nối mỗi đỉnh với trung điểm của cạnh đối diện đã xác định ở bước 1. Chỉ cần vẽ hai đường trung tuyến là đủ vì ba đường trung tuyến luôn đồng quy.
- Điểm giao nhau của hai đường trung tuyến vừa vẽ chính là trọng tâm G của tam giác. Nếu vẽ cả ba đường trung tuyến, bạn sẽ thấy chúng cắt nhau tại cùng một điểm.
Xác định trọng tâm tam giác bằng phương pháp vẽ hình học: vẽ các đường trung tuyến.
Phương pháp hình học này giúp trực quan hóa vị trí của trọng tâm và thường được sử dụng trong giảng dạy và giải các bài toán hình học phẳng trên giấy. Đối với các hình dạng phức tạp hơn hoặc khi cần độ chính xác cao, việc sử dụng phần mềm đồ họa hoặc công cụ tính toán dựa trên tọa độ sẽ hiệu quả hơn.
Ví dụ các bài toán liên quan đến tính chất trọng tâm của tam giác
Để củng cố hiểu biết về trọng tâm và tính chất của nó, hãy xem xét một ví dụ bài toán đơn giản.
Đề bài: Cho tam giác ABC có đường trung tuyến AD có độ dài bằng 9 cm. Gọi I là trọng tâm của tam giác ABC. Tính chiều dài của đoạn thẳng AI.
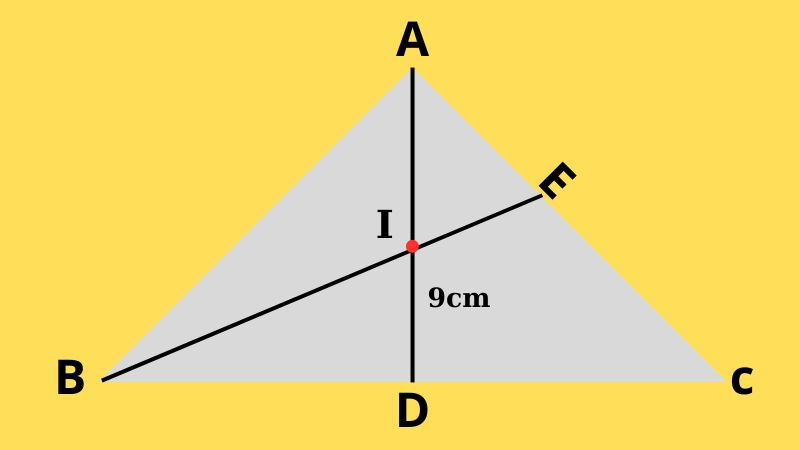Minh họa bài toán ví dụ về tính chất trọng tâm chia đường trung tuyến theo tỷ lệ 2:1.
Lời giải:
Theo định nghĩa, I là trọng tâm của tam giác ABC. Theo tính chất của trọng tâm, trọng tâm chia đường trung tuyến thành hai đoạn theo tỷ lệ 2:1, tính từ đỉnh. Nghĩa là, đối với đường trung tuyến AD, trọng tâm I nằm trên đoạn AD và AI = (2/3) AD, ID = (1/3) AD.
Đề bài cho biết độ dài đường trung tuyến AD = 9 cm.
Áp dụng tính chất tỷ lệ chia đường trung tuyến của trọng tâm, ta có:
AI = (2/3) AD
AI = (2/3) 9 cm
AI = 6 cm
Vậy, chiều dài của đoạn thẳng AI là 6 cm.
Qua bài viết này, chúng ta đã tìm hiểu rõ về khái niệm trọng tâm là gì, các tính chất quan trọng của nó trong tam giác thường và các loại tam giác đặc biệt, cùng với hai phương pháp phổ biến để xác định vị trí trọng tâm. Nắm vững kiến thức này sẽ giúp bạn tự tin hơn khi làm việc với các bài toán và ứng dụng liên quan đến trọng tâm trong hình học.
